

I y is the component of MOI in the y-axis. Let us just begin by remembering the equation for the second-moment area. This explanation will follow certain steps, such as:
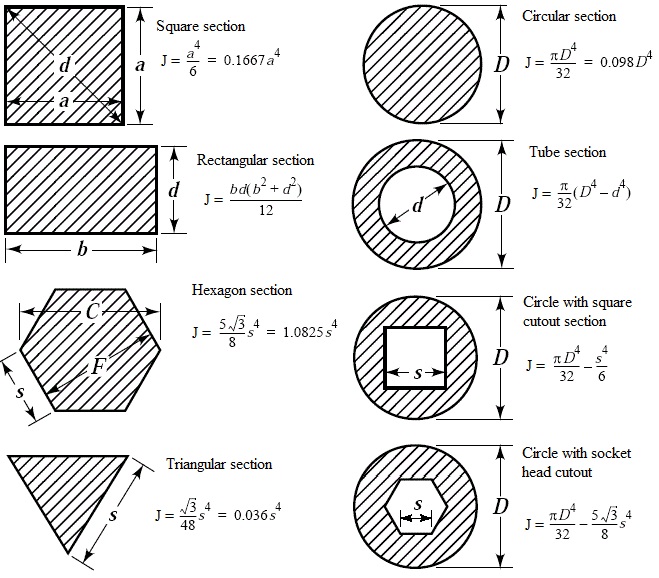
The moment of inertia formula of a circle, as per the derivation, the circular cross-section will be calculated with the radius and an axis going exactly through the center. It will be easier to understand how to find moment of inertia of a circle with this derivation. This expression for the moment of inertia of a circle about its diameter can be given asĭo you know how to find the moment of inertia of a circle? To learn about this, we need to understand the derivation of the moment of inertia of a circle, as explained below. If we consider the diameter of a circle D, then we must also take ‘r’ the radius as D/2.

Moment of Inertia of a Circle about its Diameter In the case of a quarter circle the expression is given as: In case of a semi-circle the formula is expressed as: In the case of a circle, the polar moment of inertia is given as: Similarly, the moment of inertia of a circle about an axis tangent to the perimeter(circumference) is denoted as: The moment of a circle area or the moment of inertia of a circle is frequently governed by applying the given equation: The moment of Inertia formula can be coined as: Mathematically, it is the sum of the product of the mass of each particle in the body with the square of its length from the axis of rotation. Yes, the proper definition of the moment of inertia is that a body tends to fight the angular acceleration. When a body starts to move in rotational motion about a constant axis, every element in the body travels in a loop with linear velocity, which signifies, every particle travels with angular acceleration. It can be inferred that inertia is related to the mass of a body. Sanity check: I is expected to be highest for hoop or cylindrical shell since all the mass are furthest away from the axis of rotation.First of all, let us discuss the basic concept of moment of inertia, in simple terms. Hoop or thin cylindrical shell: (R 1=R 2=R) The dA is just the area of the top of the ring, which is the area of the big (radius: r + dr) ring minus that of the smaller (radius: r) ring. We’ve introduced dV in the above equation, so, we have to find out what dV is: Now, we have to find dm, (which is just density multiplied by the volume occupied by one ring) The thickness of each ring is dr, with length L. – The cylinder is cut into infinitesimally thin rings centered at the middle. Note: the “h” in the figure should be “L”


 0 kommentar(er)
0 kommentar(er)
